I am collecting problems that start easy and then lead to a deep conversation, touching on multiple aspects of computer science fundamentals. These problems are being asked during interviews in the top technology companies, often with a twist to see if you understand the underlying principles and can adapt your solution.
Part 1: Introduction, coding practice and simple solutions
Part 2: Advanced solutions
Part 3: Expert solutions
Here we have an innocent-looking problem that bled me dry (luckily, it was not in a real interview!). Turned out, there are many interesting ways to solve it, and I thought it could be a good illustration to some fundamental algorithms. In the previous post, I covered introductions and simple (but not very efficient) solutions. This is the fun part - we will use advanced concepts like self-balancing trees, binary index trees, and the divide and conquer strategy.
There are multiple strategies to determine when a tree needs to be balanced, such as the balance factor in AVL trees or the alternation flag in red-black trees. A typical trade-off here is complexity/overhead vs. how close it gets to the perfect balance. Since we already have the number of elements in the left and right subtree, we can just use them. This approach chaises simplicity, though it may not be as efficient as the conventional methods. Solution #9 in the next post uses a height-balanced BST, and the performance is indeed better.
This solution is accepted by Online Judge for both the original and similar problem 493. So, this improved solution has linearithmic time in the worst, average and best cases.
1 Check out different implementations of self-balancing BST on this Wikipedia page.
2 It may take longer for one operation, but the overall time is proportional to the number of operations. See Amortized analysis for additional details.
3 Segment trees are a bit harder to implement, so I have them in the next part (expert solutions).
4 For a non-mutating array, you can compute the rolling sum once, and then sum ranges in a constant time.
Part 1: Introduction, coding practice and simple solutions
Part 2: Advanced solutions
Part 3: Expert solutions
Here we have an innocent-looking problem that bled me dry (luckily, it was not in a real interview!). Turned out, there are many interesting ways to solve it, and I thought it could be a good illustration to some fundamental algorithms. In the previous post, I covered introductions and simple (but not very efficient) solutions. This is the fun part - we will use advanced concepts like self-balancing trees, binary index trees, and the divide and conquer strategy.
4. Self-balancing BST with counters
So, we implemented our very own BST that can efficiently tell us how many elements are smaller than any given value (solution #3 in the previous post). The run-time complexity is O (n * h), where h is the height of the tree. For a balanced tree, the height is log n, so the complexity is linearithmic. In an unbalanced tree the height can grow up to n, resulting in the quadratic time.
To fight the quadratic time, we can balance the tree to keep its height proportional to log n [1] by performing tree rotations when inserting new elements. Tree rotations require amortized [2] constant time, so the overall run-time will be still linearithmic. We need to extend our previous solution with the rotation operations and track the number of elements in the both left and right subtrees (so that we can efficiently recalculate these numbers after the rotation).
To fight the quadratic time, we can balance the tree to keep its height proportional to log n [1] by performing tree rotations when inserting new elements. Tree rotations require amortized [2] constant time, so the overall run-time will be still linearithmic. We need to extend our previous solution with the rotation operations and track the number of elements in the both left and right subtrees (so that we can efficiently recalculate these numbers after the rotation).
There are multiple strategies to determine when a tree needs to be balanced, such as the balance factor in AVL trees or the alternation flag in red-black trees. A typical trade-off here is complexity/overhead vs. how close it gets to the perfect balance. Since we already have the number of elements in the left and right subtree, we can just use them. This approach chaises simplicity, though it may not be as efficient as the conventional methods. Solution #9 in the next post uses a height-balanced BST, and the performance is indeed better.
This solution is accepted by Online Judge for both the original and similar problem 493. So, this improved solution has linearithmic time in the worst, average and best cases.
5. Binary indexed tree (BIT)
I had an idea to arrange the input array in some intervals to count inversions efficiently. I later found that the segment tree [3] and BIT-based solutions are closest to what I had in mind. I doubt I would come up with this solution unless I knew BIT, which I didn't at the time.
The purpose of BIT (AKA Fenwick Tree) is to provide an efficient way to sum ranges in a mutating array [4]. Summation of elements in range, and update of an element both take logarithmic time. Though the concept is relatively simple, most articles I read just confused me. The name - binary index tree - is confusing by itself, as this data structure has no similarities with a binary tree whatsoever. I found this video on YouTube most helpful, and I recommend it as a practical walkthrough.
I would describe BIT as an array where each element stores a sum of a logarithmic range, defined by the element's index. First element stores sum of [1..1] elements, second - sum of [1..2] elements, fourth - [1..4], eight - [1..8] and so on. This process repeats recursively for sub-intervals [3..3], [5..7], [9..15] and so on, until the entire array is populated. Now, when we want to know, for example, the sum of first 13 elements, we need to sum elements in position 13 (binary 1101), 12 (binary 1100) and eight (binary 1000), which contain sum of elements in ranges [13..13], [9..12] and [1..8] correspondingly. Notice that we just removing the least significant bit from the index to determine the next position, resulting in no more than log n total operations.
The update operation is similar - we update all ranges that include the changed element. Such ranges can be determined by adding the least significant bit to the index. To populate BIT, you can just add elements from the original array to BIT one by one. Thus, a nice fact about BIT is that it's implementation require just few lines of code. Please keep in mind that the BIT array starts from one to keep the bit operations simple (zero element is not used, and the array size is n + 1).
Yep, that's all we need. So, how does exactly BIT help solve the problem at hand? The idea is to use numbers from the original array as indexes in BIT, and increment BIT at that index as we go through the array. We will start from the end of the array, and use the sum operation to count previously incremented, smaller indexes. There is one problem though - the original array can contain negative or very large numbers. We need to normalize the array by replacing the numbers with their relative positions; for example, [4, -100, 100000, 56] will become [2, 1, 4, 3]. We can do it by sorting numbers, and using the binary search to determine its relative position (lines 3-5 in the following snipped).
This solution is accepted by Online Judge for both the original and similar problem 493, and provides linearithmic time in the worst, average and best cases.
The purpose of BIT (AKA Fenwick Tree) is to provide an efficient way to sum ranges in a mutating array [4]. Summation of elements in range, and update of an element both take logarithmic time. Though the concept is relatively simple, most articles I read just confused me. The name - binary index tree - is confusing by itself, as this data structure has no similarities with a binary tree whatsoever. I found this video on YouTube most helpful, and I recommend it as a practical walkthrough.
I would describe BIT as an array where each element stores a sum of a logarithmic range, defined by the element's index. First element stores sum of [1..1] elements, second - sum of [1..2] elements, fourth - [1..4], eight - [1..8] and so on. This process repeats recursively for sub-intervals [3..3], [5..7], [9..15] and so on, until the entire array is populated. Now, when we want to know, for example, the sum of first 13 elements, we need to sum elements in position 13 (binary 1101), 12 (binary 1100) and eight (binary 1000), which contain sum of elements in ranges [13..13], [9..12] and [1..8] correspondingly. Notice that we just removing the least significant bit from the index to determine the next position, resulting in no more than log n total operations.
The update operation is similar - we update all ranges that include the changed element. Such ranges can be determined by adding the least significant bit to the index. To populate BIT, you can just add elements from the original array to BIT one by one. Thus, a nice fact about BIT is that it's implementation require just few lines of code. Please keep in mind that the BIT array starts from one to keep the bit operations simple (zero element is not used, and the array size is n + 1).
Yep, that's all we need. So, how does exactly BIT help solve the problem at hand? The idea is to use numbers from the original array as indexes in BIT, and increment BIT at that index as we go through the array. We will start from the end of the array, and use the sum operation to count previously incremented, smaller indexes. There is one problem though - the original array can contain negative or very large numbers. We need to normalize the array by replacing the numbers with their relative positions; for example, [4, -100, 100000, 56] will become [2, 1, 4, 3]. We can do it by sorting numbers, and using the binary search to determine its relative position (lines 3-5 in the following snipped).
This solution is accepted by Online Judge for both the original and similar problem 493, and provides linearithmic time in the worst, average and best cases.
6. Merge sort
This is a cool solution that uses the divide and conquer strategy. The intuition is like this: if we have the smallest element in the second half of the array, it will form an inversion with every element in the first half. However, it does not matter where exactly the smallest element is - just somewhere in the second half of the array. The order of elements in the first half does not matter as well to count those inversions.
Now, since order within a subarray does not matter, imagine that elements in the both halves of the array are in the sorted order. In this case, we can count inversions in linear time by using two pointers, like in the merge phase of the merge sort. When the next smallest element is in the right part, we add the count of the remaining elements in the left part to the count of inversions.
We basically need to implement a merge sort with the inversion count. We will divide the array recursively until a part contains a single element. We then will merge parts, adding inversions when the smallest element is in the right part. For the merge sort solution, however, the twist in problem #315 creates a challenge. To track inversions for each element individually, we need to introduce an index array and sort it instead. That way, we can attribute an inversion to the correct element, regardless where this element ends up after the sorting.
This solution is accepted by Online Judge for both the original and similar problem 493, and provides linearithmic time in the worst, average and best cases.
Now, since order within a subarray does not matter, imagine that elements in the both halves of the array are in the sorted order. In this case, we can count inversions in linear time by using two pointers, like in the merge phase of the merge sort. When the next smallest element is in the right part, we add the count of the remaining elements in the left part to the count of inversions.
This solution is accepted by Online Judge for both the original and similar problem 493, and provides linearithmic time in the worst, average and best cases.
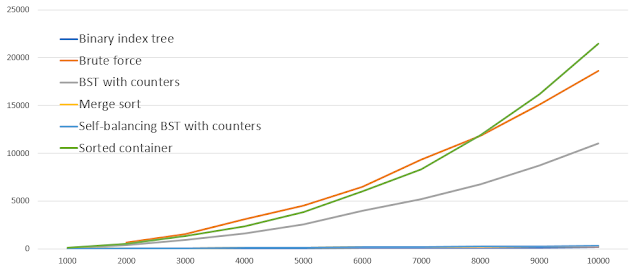
Runtime comparison
For this experiment, I generated 100 arrays with random numbers, 50 arrays with unique numbers sorted ascending, and 50 arrays sorted descending. The array size is ranging from 1,000 till 10,00 (X-axis). Then, I fed the same set of arrays to all solutions, capturing the elapsed time (Y-axis) in milliseconds.
For the advanced solutions, I ran an additional experiment with larger array sizes (10,000 - 100,000).
As you can see, Binary index tree has the best runtime, and, in my opinion, the simplest code among the advanced solutions. It does, however, require a specific knowledge, which is one of the reasons I wanted to write this post. I also ran another experiment where I got rid of the memory allocation overhead in Self-balancing BST with counters. As the result, it performed a bit better than Merge sort, but still worse than Binary index tree.
As you can see, Binary index tree has the best runtime, and, in my opinion, the simplest code among the advanced solutions. It does, however, require a specific knowledge, which is one of the reasons I wanted to write this post. I also ran another experiment where I got rid of the memory allocation overhead in Self-balancing BST with counters. As the result, it performed a bit better than Merge sort, but still worse than Binary index tree.
Practice, repeat
You will be very lucky if you get exactly this problem in an interview. Therefore, I highly recommend practicing solving a similar problem, for example, problem 493 on LeetCode.
External links
- Big O notation, Fenwick tree (AKA BIT), Self-balancing BST, Tree rotation and Amortized analysis on Wikipedia
- Tutorial: Binary Indexed Tree (Fenwick Tree) on YouTube
- Reverse pairs practice and discussion on LeetCode
- Count of Smaller Numbers After Self practice and discussion on LeetCode
- Count inversions using merge sort on GeeksforGeeks
- Count inversions using C++ set on GeeksforGeeks
- Count inversions using self-balancing BST on GeeksforGeeks
- Count inversions using binary indexed tree on GeeksforGeeks
1 Check out different implementations of self-balancing BST on this Wikipedia page.
2 It may take longer for one operation, but the overall time is proportional to the number of operations. See Amortized analysis for additional details.
3 Segment trees are a bit harder to implement, so I have them in the next part (expert solutions).
4 For a non-mutating array, you can compute the rolling sum once, and then sum ranges in a constant time.




No comments:
Post a Comment